تحليل الدارات الكهربائية في الحالة المستقرة
تحليل دارات التيار المستمر
فيما يلي سنعتمد على الطرائق المختلفة المعتمدة في حساب التيارات والتوترات في دارات التيار المستمر, ومن ثم سنعتمد على برنامج الماتلاب من أجل حل التوابع المعقدة التي يصعب الوصول لنتائجها بدون الحاسب.
يمكنكم الاطلاع على مقدمة في تحليل دارات التيار المستمر و نظرية كيرشوف في تحليل الدارات في الفيديو المرفق.
المصدر : MIT circuit course.
يمكنكم الاطلاع على مقدمة في تحليل دارات التيار المستمر و نظرية كيرشوف في تحليل الدارات في الفيديو المرفق.
المصدر : MIT circuit course.
تحليل نقاط الدارة (قانون كيرشوف الأول)
Y11V1 + Y12V2 + …….+ Y1mVm = ∑ I1
Y21V1 + Y22V2 + …….+ Y2mVm = ∑ I2
Ym1V1 + Ym2V2 + …….+ YmmVm = ∑ Im
مثال :
المطلوب إيجاد كمونات العقد للدارة المبينة بالشكل التالي :

بتطبيق قانونكيرشوف على العقد نجد :


ويكون الكود البرمجي الذي نكتبه في الماتلاب كملف M-file كالتالي :
clc
clear
Y=[0.15 -0.1 -0.05; -0.1 0.145 -0.025; -0.05 -0.025 0.075];
I=[5; 0; 2];
fprintf('Nodal Voltages V1, V2 and V3 are: \n')
v=inv(Y)*I
النتائج التي حصلنا عليها بعد التطبيق :
Nodal Voltages V1, V2 and V3 are:
تحليل حلقات الدارة (قانون كيرشوف الثاني)
Z11I1 + Z12I2 + Z13I3 + ….. + Z1nIn = ∑ V1
Z21I1 + Z22I2 + Z23I3 + ….. + Z2nIn = ∑ V2
Zn1I1 + Zn2I2 + Zn3I3 + ….. + ZnnIn = ∑ Vn
مثال :
المطلوب حساب قيمة التيار المار عبر المقاومة RB ومن ثم إيجاد الاستطاعة التي يؤمنها منبع الجهد (10v) , وذلك للدارة الموضحة بالشكل الموضح .

بتحليل الحلقات كما يبين الشكل التالي :


ويكون الكود البرمجي الذي نكتبه في الماتلاب كملف M-file كالتالي :
clear
clc
Z=[40 -10 -30; -10 30 -5; -30 -5 65];
V=[10; 0; 0];
I=inv(Z)*V;
IRB=I(3)-I(2);
fprintf('The current through R is %8.10f Amps \n', IRB)
PS=I(1)*10;
fprintf('The Power supplied by 10V source is %8.10f watts \n', PS)
النتائج التي حصلنا عليها بعد التطبيق :
The current through R is 0.0370370370 Amps
The Power supplied by 10V source is 4.7530864198 watts
The Power supplied by 10V source is 4.7530864198 watts
لنفرض لدينا منبع الجهد المبين بالشكل الموضح حيث Rs مقاومة منبع الجهد و RL الحمل.
باستخدام مجزئ الجهد نجد أن :

وللحصول على القيمة مقاومة الحمل التي تعطينا القيمة الأعظمية للطاقة نشتق معادلة الاستطاعة الأخيرة بالنسبة للمقاومة ونجعل الناتج مساوي للصفر فنجد :

وبتبسيط العلاقة الأخيرة بعد جعلها مساوية للصفر نجد : RL = Rs
ويمكن استخدام الماتلاب لمراقبة تغيير الجهد وتبديد الطاقة في الحمولة وذلك تبعاً لقيمة مقاومة الحمل.
find التابع
يستخدم هذا التابع لتحديد قيم العناصر من المصفوفة التي قيمها لا تساوي الصفر
مثال :
في الدارة الأخيرة لنفرض أن قيمة مقاومة الحمل تتغير من 0 إلى 50 كيلواوم , والمطلوب رسم تغييرات الاستطاعة في الحمل , حدد الاستطاعة العظمى على الحمل عندما .RL=10K
الكود البرمجي الذي نكتبه في الماتلاب كملف M-file كالتالي :
clc
clear
vs=10; rs=10e3; rl=0:1e3:50e3;
k=length(rl);
for i=1:k
pl(i) = ((vs/(rs+rl(i)))^2)*rl(i);
end
dp=diff(pl)./diff(rl);
rld=rl(2:length(rl));
prod=dp(1:length(dp)-1).*dp(2:length(dp));
max_power=max(pl);
fprintf('Maximum Power occurs at %8.3f ohms \n', crit_pt)
fprintf('Maximum Power dissipation is %8.5f Watts \n', max_power)
plot(rl,pl,'r-*')
title('Power delivered to load')
xlabel('load resistance in Ohms')
ylabel('Power in Watts')
النتائج التي حصلنا عليها بعد التطبيق :
Maximum Power occurs at 10000.000 ohms
Maximum Power dissipation is 0.00250 Watts

في هذه الجلسة سندرس دارات التيار المتناوب وسنستعين بالتكامل العددي للحصول على القيم الوسطية للاستطاعة. سنتطرق بعد ذلك لتحليل الدارات ثلاثية الطور وذلك بتحويلها لمجال التردد ومن ذلك الاستعانة بقوانين كيرشوف لحل الدارة. ولما سبق سنعتمد على المصفوفات من أجل حسابات التوترات والتيارات. وسنستعين بتوابع كثيرة في الماتلاب سيكون لها دور كبير في تسهيل الحسابات.
quad & quad8 التوابع
يوفر الماتلاب هذين التابعين من أجل إجراء التكامل لأي تابع والصيغة العامة للتابعين هي :
quad8(ˈfunctˈ,a,b,tol,trace)
حيث :
اسم التابع كما تم تعريفه في الماتلاب
|
funct
|
القيمة الحدية الدنيا للتكامل
|
a
|
القيمة الحدية العليا للتكامل
|
b
|
حدود التأرجح المسموح بها من أجل الدقة ولها قيمة افتراضية
|
tol
|
لتفعيل إمكانية رسم التكامل ويمكن تفعيلها بوضع أي قيمة غير مساوية للصفر
حيث أن القيمة صفر هي الافتراضية |
trace
|
مثال :
v(t) = 10.cos(120 t + 30) i(t) = 6.cos(120 t + 60)
والمطلوب تحديد القيمة الوسطية للطاقة والقيمة اللحظية للتوتر وكذلك معامل الاستطاعة وذلك بالطريقتين التحليلية والرياضية.
من أجل ذلك نكتب الكود البرمجي التالي في ملف M-file كالتالي :
clc
T=2*pi/(120*pi);
a=0;
b=T;
x=0:0.02:1;
t=x.*b;
v_int=quad('voltage1',a,b);
v_rms=sqrt(v_int/b);
i_int=quad('current1',a,b);
i_rms=sqrt(i_int/b);
p_int=quad('inst_pr',a,b);
p_ave=p_int/b;
pf=p_ave/(i_rms*v_rms);
p_ave_an=(60/2)*cos(30*pi/180);
v_rms_an=10/sqrt(2);
pf_an=cos(30*pi/180);
fprintf('Average power, analytical: %f \n average power, numerical: %f \n', p_ave_an, p_ave)
fprintf('rms power, analytical: %f \n rms power, numerical: %f \n', p_ave_an, p_ave)
fprintf('Power vactor, analytical: %f \n power factor, numerical: %f \n', pf_an, pf)
نلاحظ في البرنامج أننا استخدمنا عدة توابع ولذلك لابد من كتابتها في ملفات خاصة بها وهي كالتالي (يكتب كل تابع في ملف لوحده)
function vsq=voltage1(t)
vsq=(10*cos(120*pi*t + 60*pi/180)).^2;
end
function isq=current1(t)
isq=(6*cos(120*pi*t+30*pi/180)).^2;
end
function pt=inst_pr(t)
it=6*cos(120*pi*t+30*pi/180);
vt=10*cos(120*pi*t+60*pi/180);
pt=it.*vt;
end
النتائج التي حصلنا عليها بعد التطبيق :
Average power, analytical: 25.980762
average power, numerical: 25.980762
rms power, analytical: 25.980762
rms power, numerical: 25.980762
Power vactor, analytical: 0.866025
power factor, numerical: 0.866025
وبالتالي نجد أنه باستخدام الطريقة التحليلية أو الرقمية فإن النتائج ستكون متشابهة تماماً.
دارات التيار المتناوب الأحادية والثلاثية الطور
مثال (1)
لتكن لدينا الدارة الموضحة بالشكل:


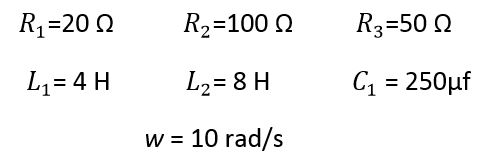
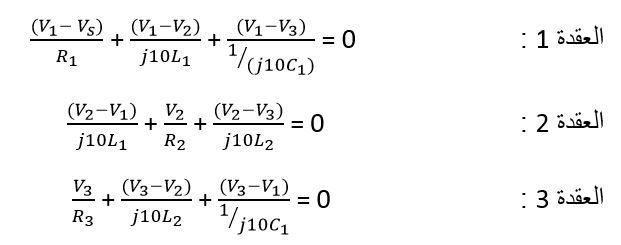
وبعد ترتيب عناصر المعادلات الثلاثة الأخيرة وإعادة تنسيقها نحصل على المصفوفة التالية :


برنامج حل المصفوفة :
clc
clear
Y=[0.05-0.0225*j 0.025*j -0.0025*j; 0.025*j 0.01-0.0375*j 0.0125*j; -0.0025*j 0.0125*j 0.02-0.01*j];
c1=0.4*exp(pi*15*j/180);
I=[c1; 0; 0];
V=inv(Y)*I;
v3_abs=abs(V(3));
v3_ang=angle(V(3))*180/pi;
fprintf('Voltage V3, magnitude : %f \nvoltage V3, angle in degree : %f \n', v3_abs,v3_ang)
النتائج التي حصلنا عليها بعد التطبيق :
Voltage V3, magnitude : 1.850409
voltage V3, angle in degree : -72.453299
v3(t) =1.85cos(10t – 72.45) v
مثال (2)
ليكن لدينا النظام غير المتوازن المبين بالشكل التالي:


والمطلوب حساب التوترات الطورية VAN , VBN , VCN .
باستخدام قانون كيرشوف نجد :
 برنامج الماتلاب :
برنامج الماتلاب :

clc
clear
Z=[6-13*j 0 0; 0 4+2*j 0; 0 0 6-12.5*j];
c2=110*exp(j*pi*(-120/180));
c3=110*exp(j*pi*(120/180));
V=[110; c2; c3];
I = inv(Z)*V;
Van=(5+12*j)*I(1);
Vbn=(3+4*j)*I(2);
Vcn=(5-12*j)*I(3);
Van_abs=abs(Van);
Van_ang=angle(Van)*180/pi;
Vbn_abs=abs(Vbn);
Vbn_ang=angle(Vbn)*180/pi;
Vcn_abs=abs(Vcn);
Vcn_ang=angle(Vcn)*180/pi;
fprintf('Phasor voltage Van, magnitude : %f \nphasor Voltage Van, angle in degree : %f \n', Van_abs, Van_ang)
fprintf('Phasor voltage Vbn, magnitude : %f \nphasor Voltage Vbn, angle in degree : %f \n', Vbn_abs, Vbn_ang)
fprintf('Phasor voltage Vcn, magnitude : %f \nphasor Voltage Vcn, angle in degree : %f \n', Vcn_abs, Vcn_ang)
النتائج التي حصلنا عليها بعد التطبيق :
Phasor voltage Van, magnitude : 99.875532
phasor Voltage Van, angle in degree : 132.604994
Phasor voltage Vbn, magnitude : 122.983739
phasor Voltage Vbn, angle in degree : -93.434949
Phasor voltage Vcn, magnitude : 103.134238
phasor Voltage Vcn, angle in degree : 116.978859
الشكل يبين شبكة خطية لها دخل x(t) وخرج y(t) .

يمكن تمثيل هذه الدخل والخرج في هذه الشبكة بالمعادلة التفاضلية التالية :

حيث :
بالانتقال إلى مستوي لابلاس تصبح المعادلة التفاضلية


وبالتالي فإن التابع الذي يعبر عن الشبكة الخطية يكون بالشكل :

وبإعادة ترتيب تابع الشبكة نحصل على الشكل التالي :

حيث :

مثال (1)


من أجل تفريق الكسر المبين نكتب مايلي :
num=[4 3 6 10 20];
den=[1 2 5 2 8];
[r,p,k]=residue(num,den)
النتائج التي حصلنا عليها عند تنفيذ البرنامج :

ويمكن العودة بشكل معاكس للتابع الأصلي بكتابة :
[num,den] = residue[r,p,k]
وستكون النتيجة في نسقين منفصلين , الأول يمثل معاملات كثير الحدود (البسط) والثاني معاملات كثير الحدود (المقام).
مثال (2)
للدارة المبينة بالشكل :


1- أوجد تابع الشبكة H(s .
2- أوجد أقطاب ورواسب تابع الشبكة .
3- إذا كانت المعادلة الممثلة لمنبع التغذية معطاة بالشكل :
 فأوجد المعادلة الممثلة للخرج vo.
فأوجد المعادلة الممثلة للخرج vo.

الحل :
بالانتقال للمستوي اللابلاسي تصبح عناصر الدارة كالتالي :



تذكر أن :

والآن سنستخدم البيئة البرمجية (ماتلاب) من أجل إيجاد الأقطاب والرواسب للتابع
clear
clc
num=[4 6 0];
den=[6 25 30 9];
disp('The zeros are : ')
z=roots(num)
disp('The poles are : ')
p=roots(den)
s1=-3+2*j;
n1=polyval(num,s1);
d1=polyval(den,s1);
vo=10*exp(j*pi*(40/180))*n1/d1;
vo_abs=abs(vo);
vo_ang=angle(vo)*180/pi;
fprintf('phasor voltage vo, magnitude : %f \nphasor voltage vo, angle in degrees : %f \n' , vo_abs, vo_ang)
النتائج التي حصلنا عليها بعد التطبيق :
The zeros are :
z =
0
- 1.5000
The poles are :
p =
- 2.2153
- 1.5000
- 0.4514
phasor voltage vo, magnitude : 3.453492
phasor voltage vo, angle in degrees : -66.990823
وبالنتيجة يكون الخرج :
الاستجابة الترددية
تعطى الصيغة العامة لتابع النقل لإشارة تمثيلية بالمعادلة :
توابع نقل شهيرة :
- مرشح تمرير منخفض


- مرشح تمرير مرتفع

- مرشح تمرير مجال


- مرشح منع مجال

حيث :


الاستجابة الترددية هي استجابة الشبكة لإشارة الدخل الجيبية , فإذا استبدلنا s=jw في تابع الشبكة نحصل على :

حيث :
وبرسم تغيرات بالنسبة للتردد نحصل على الاستجابة الترددية للطويلة وكذلك برسم تغيرات بالنسبة للتردد نحصل على الاستجابة الترددية للطور.
ويمكننا الحصول على هذه الميزات باستخدام تابع شهير في الماتلاب هو : freqs والذي تعطى الصيغة العامة له بالشكل :
hs = freqs(num,den,range)
حيث :
num = [bm bm-1 ……. b1 b0]
den = [an an-1 ……. a1 a0]
range : مجال التردد للحالة المدروسة
hs : الاستجابة الترددية بالصيغة العقدية
مثال :
من أجل الدارة المبينة بالشكل :


1- بين أن تابع النقل يعطى بالشكل :


2- إذا علمنا أن L = 5H, C =1.12µf, and R = 10000Ω بين شكل الاستجابة الترددية.
3- إذا جعلنا قيمة المقاومة R = 100Ω ما التغير الذي سيحدث , بين بالرسم.
 والآن سنستعين بالماتلاب من أجل الرسم :
والآن سنستعين بالماتلاب من أجل الرسم :

l=5; c=1.25e-6; r1=10000; r2=100;
num1=[r1/l 0];
den1=[1 r1/l 1/(l*c)];
w=logspace(1,4);
h1=freqs(num1,den1,w);
f=w/(2*pi);
mag1=abs(h1);
phase1=angle(h1)*180/pi;
num2=[r2/l 0];
den2=[1 r2/l 1/(l*c)];
h2=freqs(num2,den2,w)
mag2=abs(h2);
phase2=angle(h2)*180/pi;
subplot(2,2,1)
loglog(f,mag1,'.')
title('magniture response R=10K')
ylabel('magnitude')
subplot(2,2,2)
loglog(f,mag2,'.')
title('magniture response R=1K')
ylabel('magnitude')
subplot(2,2,3)
semilogx(f,phase1,'.')
title('phase response R=10K')
xlabel('Frequency,Hz')
ylabel('angle in fegrees')
subplot(2,2,4)
semilogx(f,phase2,'.')
title('phase response R=1K')
xlabel('Frequency,Hz')
ylabel('angle in fegrees')


تحليل الدارات الكهربائية في الحالة العابرة

1- الجهد عند تفريغ المكثف

حسب قانون كيرشوف :
حيث :
= RC الثابت الزمني
المعادلة الأخيرة تمثل معادلة الجهد عند تفريغ المكثف.
2- الجهد عند شحن المكثف

حسب قانون كيرشوف :

مثال (1) :
في حالة الشحن للمكثف , لنفرض أن C = 10
اكتب برنامج لرسم الجهد عبر المكثف في الحالات التاليتين :
- R = 1 KΩ
- R = 10 KΩ
- R = 0.1 KΩ
الحل :
Matlab Script
c=10e-6;
r1=1e3;


من أجل الدارة المبينة بالشكل , التيار المار في المحارضة معدوم , في اللحظة t=0 القاطع ينتقل من النقطة a إلى النقطة b ويبقى لمدة ثانية واحدة , وبعد ذلك ينتقل القاطع من النقطة b إلى النقطة c حيث يبقى لمدة غير محدودة , بين شكل موجة التيار عبر المحارضة بالنسبة للزمن.
tau1=c*r1;
t=0:0.002:0.05;
v1=10*(1-exp(-t/tau1));
r2=10e3;
tau2=c*r2;
v2=10*(1-exp(-t/tau2));
r3=.1e3;
tau3=c*r3;
v3=10*(1-exp(-t/tau3));
plot(t,v1,'*',t,v2,'o',t,v3,'+')
axis([0 0.06 0 12])
title('Charging of a capacitor with three time constants')
xlabel('Time, s')
ylabel('Voltage across Capacitance')
text(0.03,5, '* for R=1 kilohms')
text(0.03,6, 'o for R=10 kilohms')
text(0.03,7, '+ for R=0.1 kilohms')
والشكل التالي يبين النتائج التي حصلنا عليها من البرنامج من أجل قيم مختلفة للمقاومة ..... وهو يمثل منحني شحن المكثف .

من الشكل الناتج نستنتج أنه كلما كانت الثابتة الزمنية أكثر صغراً كلما كان زمن شحن المكثف اصغر.
مثال (2) :
في الدارة المبينة , جهد الدخل هو نبضي بإشارة مربعة لها المطال 5V وعرض النبضة 0.5s, لو كانت قيمة C = 10µF , ارسم جهد الخرج من أجل الحالات التالية :
- R = 1000 Ω
- R = 10.000 Ω
الرسم يبدأ من الصفر لينتهي زمن ثانية ونصف.

الحل :
Matlab Function
function [v,t]=rceval(r,c)
tau=r*c;
for i=1:50
t(i)=i/100;
v(i)=5*(1-exp(-t(i)/tau));
end
vmax=v(50);
for i=51:100
t(i)=i/100;
v(i)=vmax*exp(-t(i-50)/tau);
end
end
تذكرة :
يجب تسمية ملف M-file الذي يحوي تابع بنفس اسم التابع لكي يعمل .
Matlab Script
c=10.0e-6;
r1=2500;
[v1,t1] = rceval(r1,c);
r2=10000;
[v2,t2] = rceval(r2,c);
plot(t1,v1,'+r',t2,v2,'*k')
axis([0 1 0 6])
title('Response of an RC circit to pulse input')
xlabel('Time, s')
ylabel('voltage, V')
text(0.65,5.5,'+ is for 2500 ohms')
text(0.65,5.0,'* is for 10000 ohms')
والشكل الناتج (المبين بالشكل)يبين منحني الشحن والتفريغ للمكثف .

الحالة الأولى

حسب قانون كيرشوف :

حيث تعطي علاقة الثابت الزمني :

إن المعادلة الأخيرة تمثل الاستجابة الطبيعية لدارة RL.
الحالة الثانية

حسب قانون كيرشوف :

الجهد عبر المقاومة :
الجهد عبر المحارضة :

مثال :
الحل :
- من أجل 0 < t < 1 s , نستخدم المعادلة :

حيث :
- عند اللحظة t = 1 s :

- من أجل t > 1 s :

Matlab Script
tau1 = 200/100;
for k=1:20
t(k)=k/20;
i(k)=0.4*(1-exp(-t(k)/tau1));
end
imax=i(20);
tau2=200/200;
for k=21:120
t(k)=k/20;
i(k)=imax*exp(-t(k-20)/tau2);
end
plot(t,i,'o')
axis([0 6 0 0.18])
title('Current of an RL circuit')
xlabel('time , s')
ylabel('Current, A')

من أجل الدارة المبينة بالشكل , وباستخدام قانون كيرشوف نكتب :

بمفاضلة المعادلة المبينة نحصل على المعادلة :

يمكن الحصول على الحل المتجانس لهذه المعادلة كالتالي :

ويمكن كتابة هذه المعادلة بالشكل :

وجذور المعادلة يمكن الحصول عليهم بسهولة وبفرض الجذور :

فإن حل المعادلة السابقة يكون :

مثال :
للدارة السابقة لنفرض أن :

والمطلوب إيجاد التيار .
الحل :
بجعل Vs=0 نكتب المعادلة :

وباستخدام الماتلاب يمكن إيجاد جذور هذه المعادلة :
Matlab Script
A=[1 40 1000];
root_A=roots(A)
root_A =
-20.0000 +24.4949i
-20.0000 -24.4949i
وبعد أن حصلنا على الجذور يمكن كتابة علاقة التيار كما يلي :

وبالنتيجة :
يمكن الاستعانة بتحويلات لابلاس من أجل الحصول على التوترات والتيارات في الدارات الأكثر تعقيداً و الجدول التالي يبين تحويل لابلاس لمجموعة من التوابع.

رباعيات الأقطاب
سأكتفي بمثال لشرح رباعيات الأقطاب.
مثال :
بفرض إن مكبر العمليات الوضح بالشكل هو مثالي فالمطلوب :

1- أوجد العناصر الأساسية لمصفوفة الممانعات z.
2- إذا كانت الشبكة موصلة بمنبع جهد بحيث مقاومته الداخلية 50Ω ومقاومة الحمل 1kΩ, أوجد نسبة التكبير.
3- باستخدام الماتلاب ارسم الاستجابة الترددية للمطال.
باستخدام قانون كيرشوف نجد :
.png)
من المعادلتين الأخيرتين :
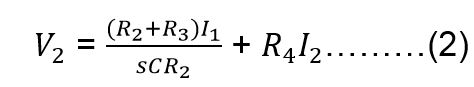
من المعادلتين 1-2 نجد :

ولإيجاد نسبة التكبير :

ومن أجل الرسم باستخدام الماتلاب نكتب البرنامج التالي :
clc
clear
num=[2];
den=[1.05e-4 1];
w=logspace(1,5);
h=freqs(num,den,w);
f=w/(2*pi);
mag=20*log10(abs(h));
semilogx(f,mag);
title('Lowpass Filter Response')
xlabel('Frequency,Hz')
ylabel('Gain in dB')











خارج الموضوع تحويل الاكوادإخفاء الابتساماتإخفاء